Système solaire

Pour créer un système stellaire, il nous faut premièrement des images.

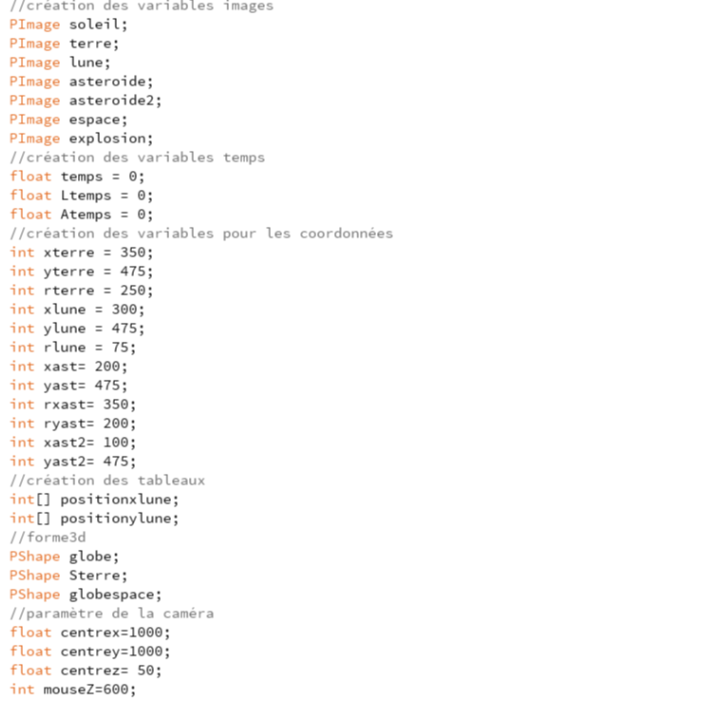
Sur l'image ci-dessous, nous créons les différentes variables d'images avec la fonction "PImage" puis nous leur affectons une image avec la fonction "variable=loadImage(...)". Nous avons donc importer nos images.

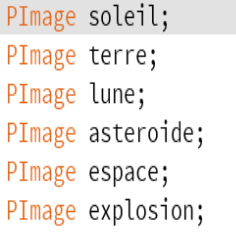
Nous avons nos images mais il faut les placer, et pour cela nous devons utiliser la fonction "image" de la sorte "image(variable, coordonnée x, coordonnée y, taille x, taille y)".

Exemple avec l'image ci-dessous.

          Attention : les coordonnées ne correspondent pas avec le centre d'une image mais au coin supérieur gauche, il faut donc soustraire aux coordonnées la moitié de la taille)               (coordonné x - taille x/2).

Normalement nous devrions avoir ça :

          PS: Il ne faut pas oublier de mettre le fond derrière (important pour la suite).

Les images sont toute afficher c'est bien mais il nous reste à les animer pour cela il faut remplacer les coordonnées par des variables.

Sur l'image ci-dessus, la fonction "int" permet permet de créer une variable entière nous permettant de créer nos variable x et y. Mais nous devons rajouter la variable r(terre/lune/astéroïde) qui correspond au rayon de la trajectoire voulue. PS: l’astéroïde à 2 variable r car nous voulons faire un ovale et non un cercle comme avec la Terre et la Lune.

Ensuite on remplace ces variables par les coordonnées précédente.

Nous avons affecté des variables aux coordonnées mais elle n'ont pour l'instant qu'une seule valeur statique, or pour animer notre système solaire il faut que ces valeur change.

Nous allons donc utiliser la formule des ellipses et l'appliquer à nos coordonnées de la façon suivante: 

          La formule s'exécute de la sorte "variable x= (int)(centre x + rayon x * cos(variable temps))" pour les coordonnées x et "variable y= (int)(centre y +rayon y * sin(variable temps)". le "(int)" indique que l'on veut un résultat entier et non décimal.

Si vous êtes attentif vous aurez remarqué 2 choses, la première est que les centres x et y de la Lune sont les coordonnées de la Terre, c'est normal car on veut que la Lune tourne autour de la Terre.

La deuxième choses est la variable "temps". Cette variable va permettre de régler la vitesse de nos objets. Mais il nous faut les créer comme on la fait avec les variables X et Y sauf que là, la fonction utilisé n'est pas "int" mais "float" car nous voulons une variables à décimal.

Ensuite nous allons devoir régler ce temps:

          La fonction "millis()" va nous permettre d'obtenir des milliseconde que l'on va diviser afin de régler la vitesse. Important, le dénominateur doit être un décimal comme sur l'image sinon notre animation seras saccadé. 

Résultat vous devez obtenir le programme suivant: 

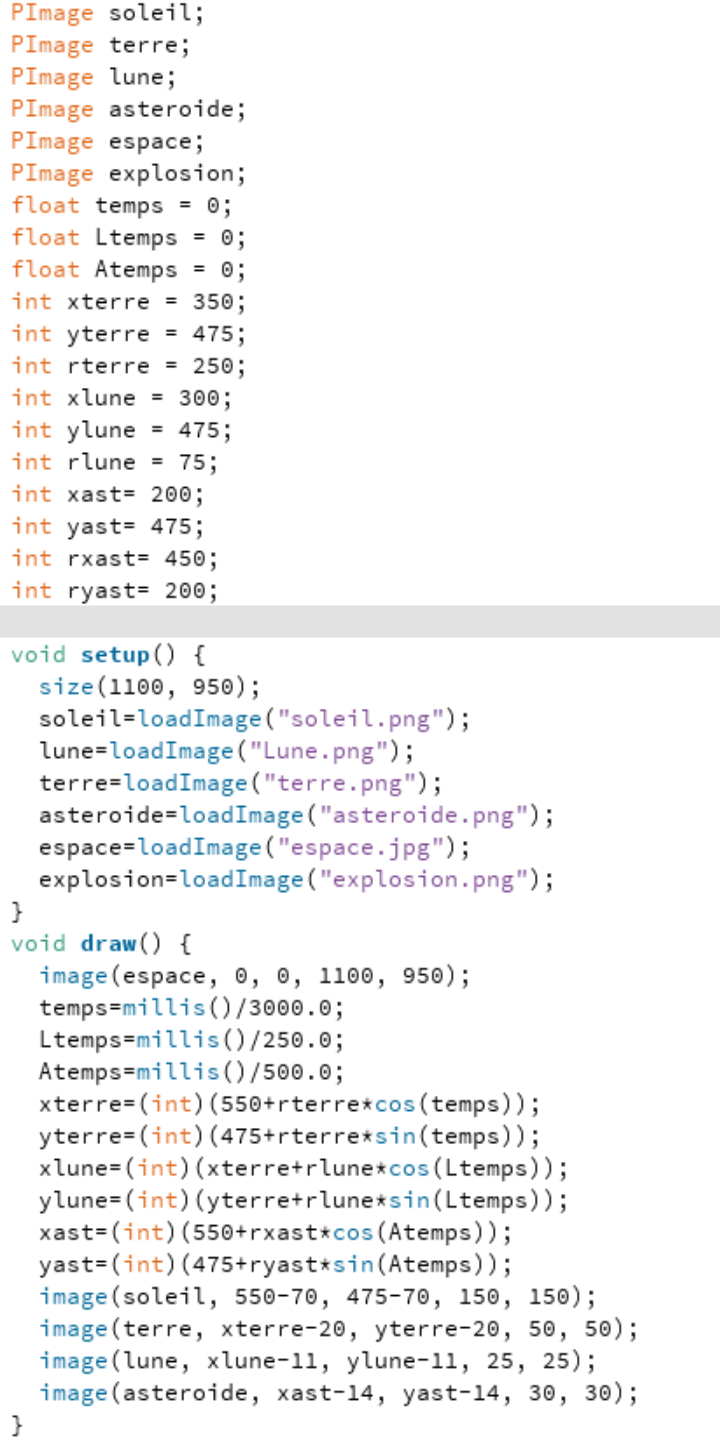
Maintenant que notre système marche, nous allons l'améliorer en commençant par le tracer des trajectoires.

Pour la Terre et les astéroïdes nous allons juste afficher des ellipses car leur trajectoire sont simple. Pour ce faire, nous allons utiliser 3 fonctions "noFill()", stroke(...)",               "ellipse(centre x, centre y, rayon x*2, rayon y*2)".

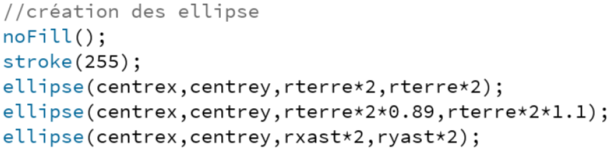
               Ici, la fonction "noFill()" va permettre de créer des figures vide et "stroke(255)" va changer la teinte de la figure (0= noir et 255= blanc).

Nous avons donc les trajectoires de tous nos astres sauf un : la Lune. Le problème c'est que la trajectoire de la Lune est bien trop complexe pour être tracé avec une simple fonction, nous allons donc devoir tracer son parcours point par point à l'aide de tableau.

               "int[] variable" va comme vous vous ne douter créer une variable tableau mais il y a un inconvénient, c'est que ce tableau est vide c'est à dire qu'il n'y a aucune case libre pour y entré des valeurs, on ne peut donc pas l'utiliser d'une quelconque manière. Il faut donc créer une ou plusieurs case dans ce tableau avec "new int [nombre de case]". 

                PS: dans notre cas on ne sait pas combien il nous faut de case pour tracer la trajectoire de la Lune et étant donné que plus le tableau est grand plus il alourdit la charge du programme on met le tableau à 0 case (0 ne correspond pas au vide évoqué précédemment pour l'ordi).

Avec ces tableaux nous allons devoir mettre la position de la Lune à chaque étape, pour ce faire utilisons "append(...)" dans la fonction "draw()".

               Comme nous pouvons le voir sur l'image, "append" n'est pas une fonction mais une affectation ce qui veut dire que nous devons d'abord placer la variable voulue puis utiliser "append" pour lui créer une nouvelle case avec un valeur prédéfinie. Ce qui donne :                 "tableau=append(tableau, valeur/variable)", ici les valeur sont les variables contenant la position de la Lune. 

Il nous reste plus qu'a dessiner ses fameux point et nous aurons notre trajectoire. Servons nous donc des boucles.

               La boucle "for marche de la façon suivante "for (variable1 ; variable1 =>< varable2/valeur ; variable1+1)". En bref ce que l'ordi va comprendre c'est pour la variable i tant que i < à la variable positionxlune-1 faire... et à la fin de chaque étape rajouter 1 à la variable i. De plus, le ".length" après la variable du tableau sert à transformer la variable tableau en variable entière correspondant au nombre de case du tableau.

               Après, je ne pense pas avoir besoin de définir la fonction point mais le [i] doit vous interpeller, il correspond à un la case qui doit être du tableau qui doit être exploité, ici il correspond au nombre de la variable i.

Nous avons donc toute les trajectoires de tous nos astres mais nous pouvons aller plus loin, nous pouvons construire notre système solaire en 3D.

Il nous faut pour cela rajouter un paramètre à notre fonction "size()", le paramètre P3D.

Notre système est donc maintenant en 3D mais il nous reste à l'exploiter, commençons par créer des sphère correspondant à notre soleil et notre espace. Nous allons procéder en trois étapes, la création des variables de forme géométrique, l'affectation de sphère à ces variables ainsi que leur texture et  afin leur placement.

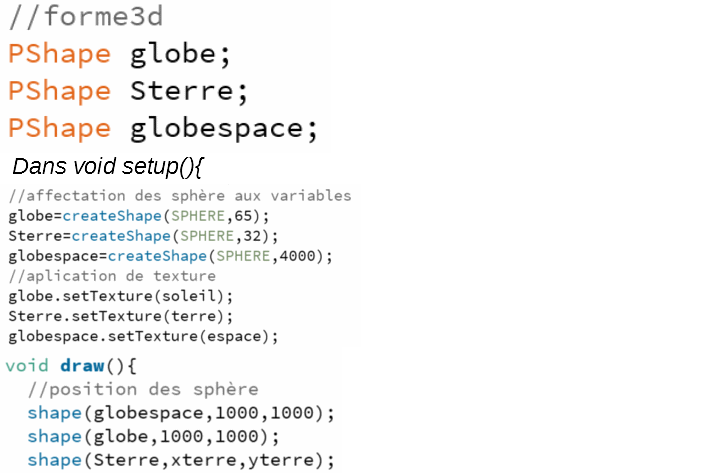
               Nous avons donc "PShape"pour créer des variables pour forme géométrique, "createShape(forme,taille)" pour l'affection de forme, ".setTexture(image)" pour l'affectation d'une image à la sphère (attention à avoir un image convenable), et la fonction "shape(variable, coordonné x, coordonné y)" pour positionner et afficher nos sphères dans l'espace.

               PS: N'oublier pas de supprimer le fond d'écran en 2d car nous l'avons remplacé par la sphère globespace.

Notre système est maintenant prêt pour pouvoir mettre une caméra mobile. Dans un premier temps plaçons une caméra de base dans "void setup(){".

                La caméra contient 9 paramètre, les 3 premiers correspondent au placement de la caméra dans l'espace, les 3 suivant sont la où pointe la caméra c'est à dire le centre, les 3 dernier corresponde la ou s'axe la caméra.

Il nous faut maintenant une caméra mobile, c'est à dire une caméra qui se réactualise dans "void draw(){".

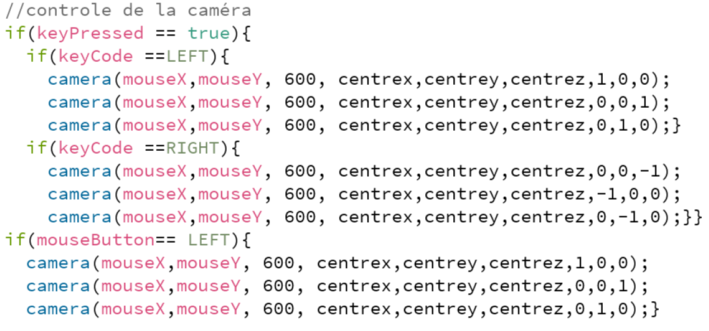
               Ici les conditions servent pour le contrôle temporaire des caméras, vous pouvez très bien les supprimé. Les variables "mouseX" et "mouseY" correspondent au coordonné de la souris, "KeyPressed" correspond à si une touche du clavier est pressé, "KeyCode" est une variable qui ne prend en compte que certaine touche du clavier, "mouseButton" marche de la même manière que "KeyCode" mais pour la souris. 

Nous avons donc un système 3D opérationnel avec ce programme: 

Poussons le vice encore plus loin en transformant tout les astres en forme 3d et en modifiant leur trajectoire de la verticale à l'horizontale. Et à la fin programmons la collision.

Pour commencez retaper les même étape qui on permis de faire de la terre une boule pour la lune et les astres.

               PS: pensez à rajouter la fonction "noStroke()" avant la création des sphères dans "setup()".

Maintenant faisons tourner le soleil sur lui même. 

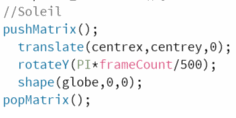
          Pour faire tourner le Soleil nous utilisons la fonction "pushMatrix(); ......; popMatrix();" qui permet de faire des modifications n'affectant pas le reste du programme.

          Dans ce fonction Matrix nous modifions l'origine du repère du système au centre du soleil puis nous faisons pivoter l'axe Y dans le dans grâce à la variable frameCount puis nous affichons l'objet soleil (ici globe).

               Pour la Terre le positionnement de l'origine est différente. la coordonné x reste la même mais vue que pour passez de verticale à l'horizontale on place les coordonnées y de la Terre dans l'axe z et on lui soustrait la même valeur que le centre de votre système. Quand à l'axe y, la valeur est le centre y de votre système. Le reste est pareil que pour le Soleil.

Pour la Lune le fonctionnement est le même que pour la Terre.

Par contre pour les astéroïdes on va compliquer la tâche en inclinant leur trajectoire. 

               Commençons par parler de l'origine, pour l'axe x et z c'est pareil qu'avant, par contre pour l'axe y vous devez remettre la coordonnée x de votre astéroïde que vous multiplié par PI/entier , vous mettez la valeur que vous voulez dans l'entier. Après dans la fonction "Shape()", les 3 premier paramètres sont toujours les mêmes par contre on rajoute 2 autre paramètre, la taille X et Y qui permette de modifier notre sphère en une sorte de cylindre sphérique.

Bon maintenant que nos astres tournent, il faut aussi remettre nos ellipse en place.

          Commençons avec la Terre, l'origine ne sont plus les coordonnées de l'astre mais celle du centre de votre système, la rotation se fait sur l'axe X avec pour paramètre PI/2 qui permet de faire de passer de horizontale à verticale. Le "stroke()" permet de donner une couleur à la trajectoire afin de la reconnaître parmi les autres. enfin dans la fonction ellipse n'oubliez pas d'affecter les 2 premier paramètre à la valeur 0 afin de ne pas doubler la position du centre de l'ellipse.

          Pour la Lune, effectué la même chose que pour la Terre, et remplacer la fonction "ellipse()" de la terre par le tracer de point que nous avons créé ultérieurement. 

          Enfin pour les astéroïdes, c'est exactement la même chose que pour la Terre sauf que vous rajouter une rotation de l'axe Y correspondant au PI/entier utiliser pour la coordonné Y de l'origine de votre Sphère.

Il ne nous reste plus qu'a programmer la collision:

          Pour notre collision nous avons besoin de savoir quand notre astéroïde entre en collision avec la Terre, pour cela utilisons 2 conditions, une condition vérifiant pour les coordonnées X et une autre pour Y. Dans la condition nous vérifions dans un premier temps si le centre de la sphère de l'astéroïde est supérieur au centre de la sphère de la Terre moins une certaine valeur (correspondant au rayon de votre sphère) puis on vérifie si le centre de la sphère de l’astéroïde est inférieur au centre de la Sphère de la Terre plus la valeur du rayon. Nous obtenons donc (si on se le représente mentalement) un cube ou dès que le centre de l’astéroïde entre dedans on exécute le programme suivant: afficher le texte aux coordonnées X,Y,Z

          PS: si vous voulez vous pouvez rajouter "noLoop()" à la fin afin d’arrêter le programme marquant ainsi la collision de façon plus poussé. Après vous pouvez afficher une image lors de la collision, dans ce cas vous placé la fonction "image(...)" au début de votre condition est vous bidouiller avec ces coordonnées afin de placer l'image à l'endroit voulue.